Minicurso Octave/Matlab¶

Prof. MsC. Carlos de Castro

Bem vindos ao minicurso de Octave/Matlab.

Conhecendo o programa ¶

GNU Octave é uma linguagem de alto nível, construída inicialmente para computação numérica. Ela provê uma interface de linha de comando para resolver problemas lineares e não lineares numericamente e executa outros experimentos numéricos que são compatíveis com MATLAB.

A imagem a seguir é a interface do MATLAB e OCTAVE.

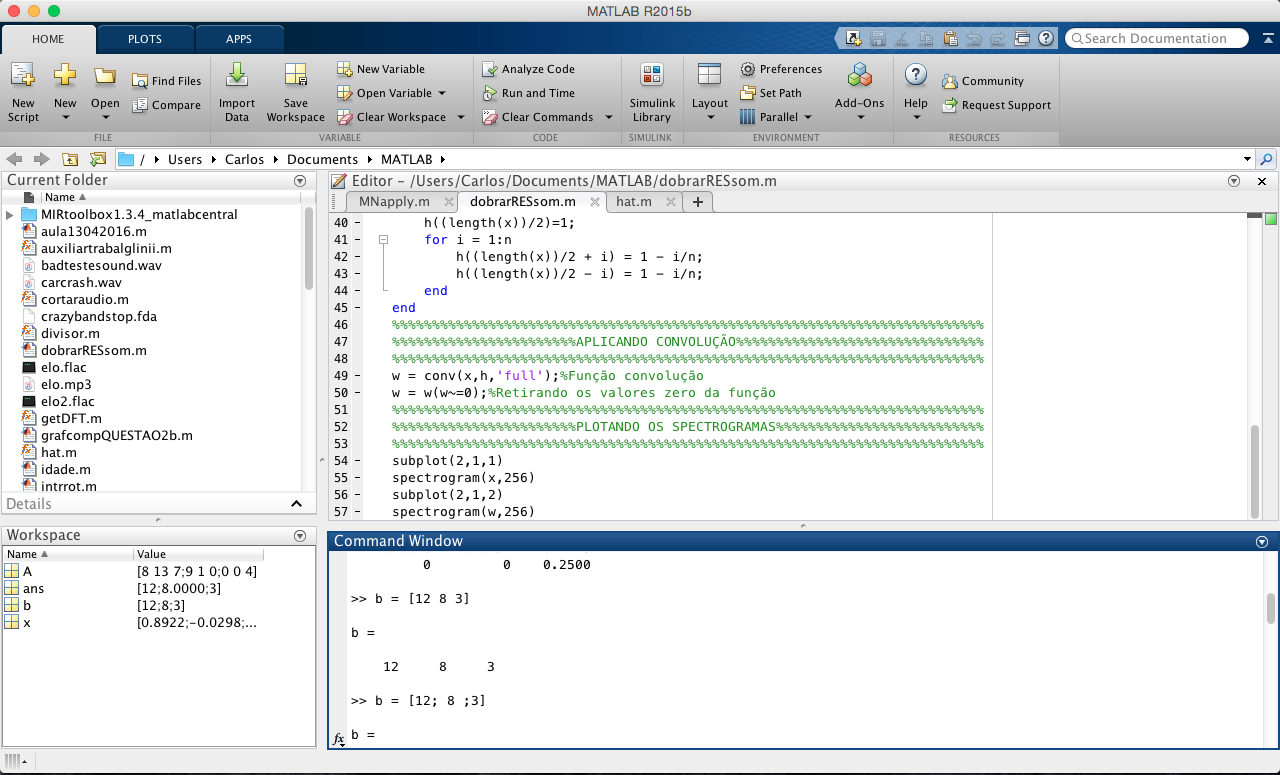
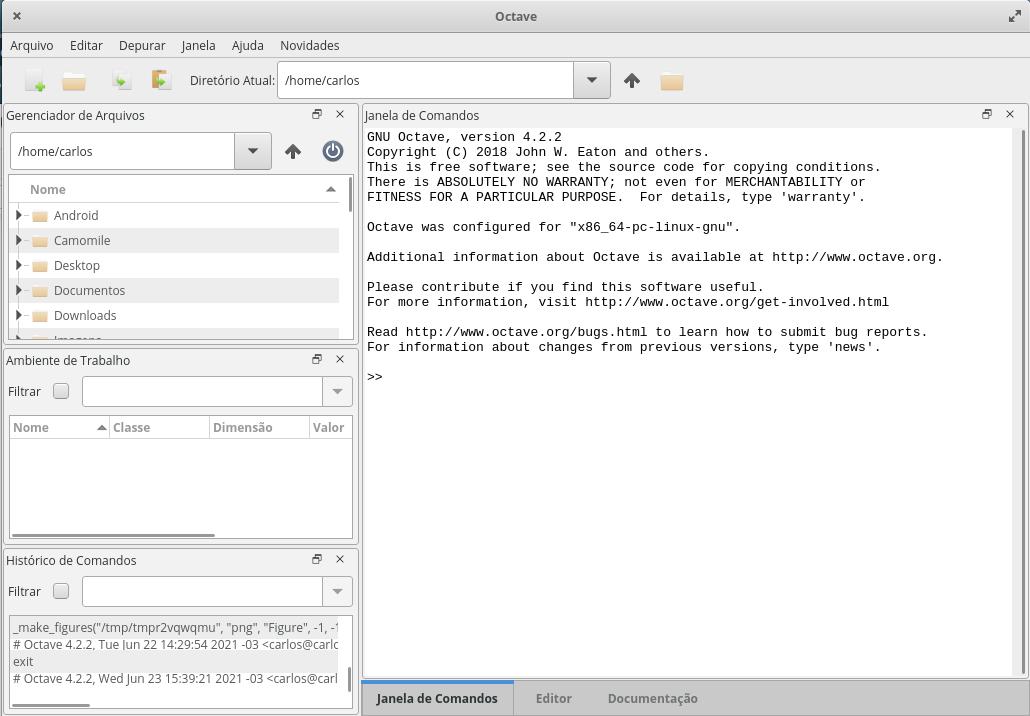
Instalação ¶

Acessar Site (lá tem tudo o que precisa saber, para todos os sistemas operacionais).

Principais janelas ¶

Gerenciador de arquivos¶

É o local onde estarão os scripts e funções que você irá desenvolver para o Octave. Você pode alterar a localização da pasta, navegando no gerenciador.

Janela de Comandos¶

É o local onde onde podemos escrever e executar os programas, funções e fórmulas matemáticas.

Editor¶

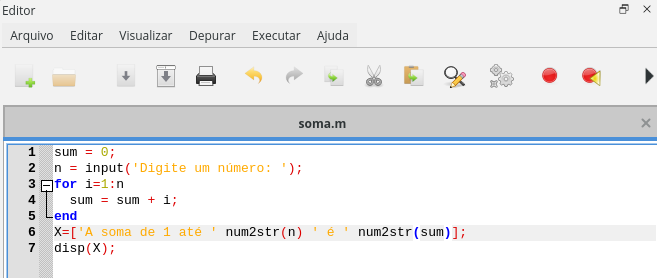
No editor é onde você escreve seus scripts e funções, e salva-os na pasta. Esse arquivo salvo terá extensão .m e aparecerá no gerenciador de arquivos (caso você salve lá). Você poderá executar suas funções chamando-as pelo nome na Janela de comandos ou clicando com o botão direito no arquivo, em gerenciador de arquivos, e clicar em Executar.

	Para criar um script novo, clique no botão que fica no canto superior esquerdo, com o nome de Novo script

Ambiente de Trabalho¶

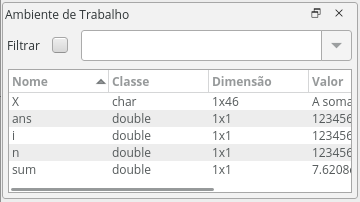
Essa janela irá aparecer todas as variáveis que estão ativas. Nele você pode ver o nome da variável, a classe (se é char - caractere, double - ponto flutuante real com dupla precisão, int - inteiro, etc), a dimensão ($1\times 3$ - vetor 'deitadinho' de 1 linha e 3 colunas) e o valor.

Histórico de comandos¶

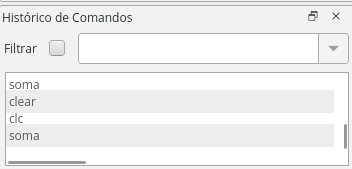
Nesse ambiente, você poderá ver o histórico de comandos feitos, desde o momento da primeira abertura do programa.

Janela de troca de ambiente¶

Essa janelinha fica logo abaixo do editor ou da Janela de Comandos. Nela, você consegue trocar entre esses ambientes.

Aqui no Notebook, tanto os scripts, quanto a janela de comando são representadas na mesma célula, como a que vemos abaixo:

Na janela do octave:

Aqui no Jupyter, posso fazer tudo em uma mesma célula:

Ou podemos fazer separadamente, pra ficar igual à janela de comando.

Como as células aqui do Jupyter são a mistura do editor de funções com a janela de comando, vamos utilizar apenas uma célula, quando conveniente, a partir de agora. :)

Caso queira rodar o kernel do Octave no Jupyter Notebook, acesse o git: https://github.com/Calysto/octave_kernel e veja como instalar no seu computador. Caso ainda não tenha jupyter, instala o Anaconda por aqui https://anaconda.org/anaconda/jupyter e volta lá no Git do Octave_kernel para instalar.

Perceberam uma coisa interessante? O caractere ; faz com que você controle o que aparece ou o que não aparece na janela de comando. Vamos fazer um teste.

Na célula a seguir, vou fazer uma soma em looping, ou seja, vou pedir pro octave fazer uma soma de números naturais, de 1 até um n determinado. Para isso, usarei um loop for, que veremos mais pra frente.

Apareceu um monte de coisa que eu não queria. Como fazer para não aparecer?

Operações básicas ¶

*jajá veremos para que isso serve.

Formato de número em ponto flutuante¶

Ao trabalhar com ponto flutuante (double ou float), é possível obter diversas visualizações desses números com o Octave. A seguir, vemos uma lista de alguns formatos possíveis:

Alguns comandos interessantes¶

• help: Ao digitar >> help <function> na janela de comando do octave/matlab, aparecerá na mesma janela os detalhes acerca da função procurada.

Exemplo¶

• lookfor: O comando lookfor procura por um determinado texto na biblioteca do Octave/MatLab.

Exemplo¶

- Clc e Clear: O comando Clc e Clear apagam as informações da Janela de comando e da lista de variáveis no "Ambiente de trabalho", respectivamente.¶

• Who: lista todas as variáveis do "Ambiente de trabalho";
• Quit: Sai do Octave/Matlab

Outros comandos¶

Matrizes e vetores ¶

A construção de matrizes e vetores no Octave já está inclusa na instalação padrão do programa. Na sintaxe, o vetor é representado como um conjunto de números, separados em linhas e colunas, organizados entre [], de modo que:

• A separação por espaço ` ou vírgula,` representa números em uma mesma linha da matriz;
• A separação por ;, nesse caso, representa números em diferentes linhas.

Exemplo¶

1) Para construir um vetor linha $x$, basta criar a lista com seus elementos separados por , ou por espaço :

Exemplo¶

2) Para construir um vetor coluna $y$, basta criar a lista com seus elementos separados por ;: (não se preocupe, o ponto e vírgula no final do vetor continua existindo).

Exemplo¶

3) Para construir uma matriz $M$ de 3 linhas e 4 colunas, teremos que usar todos os separadores vistos anteriormente:

Obs: O Octave/Matlab aceita variáveis como entrada das matrizes.

Exemplo¶

Vetores linearmente espaçados¶

Na Álgebra Linear, Processamento de Sinais, Análise Numérica, etc, é comum utilizar de vetores com uma padronização entre os seus elementos. Essa padronização pode ser obtida de algumas maneiras, especialmente

• vetores linearmente espaçados, isto é, a se $x=[x_1, x_2, \cdots, x_k]^T$, então $x_i-x_{i-1}=r, r\in \mathbb{R}$ e $\forall i \in [1,k].$

A sintaxe para criar esses vetores é simples: Se quisermos um vetor $x$, indo de $n\in\mathbb{R}$ até no máximo $m\in\mathbb{R}$, com a distância entre seus elementos $q\in\mathbb{R}$, basta fazermos $$x=[n:q:m].$$

Exemplo¶

• Vetores linearmente espaçados, determinado o número de elementos do vetor.

Aqui, usaremos a função >>linspace(n, m, N), em que $n\in\mathbb{R}$ é o primeiro elemento do vetor, $m\in\mathbb{R}$ é o último elemento do vetor e $N\in \mathbb{N}$ é o número de elementos do vetor.

Exemplo¶

OBS: Veja que os dois métodos construíram vetores diferentes, com o mesmo número de elementos e determinados o mesmo $n$ e $m$.

Acessando elementos de matrizes e vetores¶

Dada uma matriz $$A=\left(\begin{array}{ccc} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array}\right)$$ como podemos acessar os elementos da matriz? Isto é, caso precisamos obter o elemento que se encontra na linha 3, coluna 2 da matriz, acessamos a partir do Octave.

As sintaxes para acesso dos elementos de matrizes $(M\in\mathbb{C}^{n\times n})$ e vetores $(v\in\mathbb{C}^n)$, para algum $n\in \mathbb{N}$, no Octave/Matlab é $$M/v(\ell,c),$$ em que $\ell,c\in\mathbb{N}$ são os índices da(o) matriz/vetor. No caso de vetores, a sintaxe pode ser tanto $$v(\ell,1)\text{ ou }v(\ell) \text{ (para o caso de vetor coluna)}$$ ou $$v(1,c)\text{ ou }v(c) \text{ (para o caso de vetor linha)}.$$

Para acessar linhas ou colunas inteiras, ou até partes da matriz, é possível utilizar as sintaxes:

• $M(:,c)\text{ (para acessar todos os elementos da coluna $c$ - resultando em um vetor coluna com $n$ elementos)}$
• $M(\ell,:)\text{ (para acessar todos os elementos da linha $\ell$ - resultando em um vetor linha com $n$ elementos)}$
• $M(a:b,p:q) \text{(para acessar os elementos que estão entre as linhas $a$ e $b$ as colunas $p$ e $q$ - resultando em uma matriz $M'\in\mathbb{R}^{(b-a)\times (q-p)}$)}$

Voltando à matriz $A$, podemos criar o seguinte esquema:

Antes de passarmos para operações entre matrizes e vetores, vamos fazer uns exercícios.

Obs: Para excluir uma linha ou coluna de uma matriz, basta fazer $M(:,p) = []$ (para excluir a $p$-ésima coluna da matriz, ou $M(q,:)=[]$ para excluir a $q$-ésima linha.

Exercícios¶

1) Escolha $m,n\in \mathbb{N}$, $3 \leq m,n \leq 10$ para criar uma matriz aleatória $M\in\mathbb{R}^{m\times n}$.

2) Altere a primeira coluna e a primeira linha da matriz por um vetor com números aleatórios de $0$ a $1$ (utilize a função $rand()$).

3) Escolha uma submatriz $M'\in \mathbb{R}^{2\times 2}$ da sua matriz $M$ e substitua por uma matriz de identidade $I_{2\times 2}$ (Use a função eye$(\cdot)$).

4) Altere o elemento da linha $m-2$ e coluna $2$ para o número $NUM=randi(m*n)$ (randi é uma função que devolve um número inteiro aleatório de $0$ a $m\cdot n$).

5) Separe sua matriz $M$ em vetores coluna e vetores linha. (por exemplo, se $$M=\left(\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right),$$ então teremos os vetores coluna $$c1=\left(\begin{array}{c} 1 \\ 4 \\ 7 \end{array}\right),c2=\left(\begin{array}{c} 2 \\ 5 \\ 8 \end{array}\right)\text{ e } c3=\left(\begin{array}{c} 3 \\ 6 \\ 9 \end{array}\right)$$ e os vetores linha $$\ell1=\left(\begin{array}{ccc} 1 & 2 & 3 \end{array}\right),$$ $$\ell2=\left(\begin{array}{ccc} 4 & 5 & 6 \end{array}\right)\text{ e } $$ $$\ell3=\left(\begin{array}{ccc} 7 & 8 & 9 \end{array}\right).\left. \right)$$

Operações com matrizes e vetores ¶

Para efetuar operações com matrizes e vetores, é preciso ter um pouco de cuidado. Devemos, aqui, lembrar da álgebra linear antes de sair fazendo produto de vetores e matrizes.

Lembrando que em um espaço vetorial $V$ qualquer definido sobre um corpo $\mathbb{K}$, definimos a soma e o produto por escalar entre os elementos desse espaço, isto é, se $v,w \in V$ e $V$ é um espaço vetorial, então $v+w \in V$ e $\lambda v \in V$, qualquer que seja $\lambda \in \mathbb{K}$. Da mesma forma, o Octave/Matlab não vai saber o que fazer se eu pegar $v \in V$ e $w \in W$, com $V$ e $W$ espaços vetoriais tais que $W\cap V = \emptyset$ e fizer $v+w$ ou $w \cdot v$.

Podemos definir, aqui, algumas operações possíveis entre vetores, matrizes e escalares.

Se $v=(v_1 \ v_2 \ \cdots \ v_n)^T$ e $w=(w_1 \ w_2 \ \cdots \ w_n)^T$ e $\lambda \in \mathbb{C}$:

• $v+w= (v_1+w_1 \ v_2+w_2 \ \cdots \ v_n+w_n)^T$ (no octave, utiliza-se $v+w$ para efetuar a soma).
• $\lambda v = (\lambda v_1 \ \lambda v_2 \ \cdots \ \lambda v_n)^T$ (no Octave, utiliza-se $\lambda \ast v$ para efetuar a operação).
• $v \odot w = (v_1w_1 \ v_2w_2 \ \cdots \ v_nw_n)^T$ (esse produto é conhecido como Produto de Hadamard e, no Octave, utiliza-se $v.\ast w$).
• $v^T=(v_1 \ v_2 \ \cdots \ v_n)$ (a operação de transposição de um vetor pode ser feita utilizando ', isto é, $v'$.
• $\langle v, w \rangle = v \cdot w = \sum_{i=1}^{n} v_iw_i$ (o produto interno pode ser calculado, no matlab, utilizando a função $dot(v,w)$ ou, $v'\ast w$.

obs: Se $v\in \mathbb{C}^n$ e $w \in \mathbb{C}^m$ e a operação $\langle v, w \rangle = v^Tw$ resulta em um número real, o que acontece se fizermos $vw^T$? Ainda é possível fazer essa operação, mas o resultará em uma matriz que mora em $\mathbb{C}^{n \times w}.$ Por exemplo: se $v=(1 \ 2 \ 3)^T$ e $w=(4 \ 3 \ 2 \ 1)^T$, então $$vw^T=\left(\begin{array}{cccc} 4 & 3 & 2 & 1 \\ 8 & 6 & 4 & 2 \\ 12 & 9 & 6 & 3 \end{array}\right).$$ Ou seja, se $v=(v_1 \ v_2 \ \cdots \ v_n)^T$ e $w=(w_1 \ w_ 2 \ \cdots \ w_m)^T$, então $$ vw^T=\left(\begin{array}{ccc} \rule{12pt}{.6pt} & v_1w & \rule{12pt}{.6pt} \\ \rule{12pt}{.6pt} & v_2w & \rule{12pt}{.6pt} \\ & \vdots & \\ \rule{12pt}{.6pt} & v_nw & \rule{12pt}{.6pt} \end{array}\right).$$

Vejamos:

As operações válidas para matrizes são:

• Se $M\in\mathbb{C}^{m\times p}$, $N\in\mathbb{C}^{p\times n}$ então $MN\in \mathbb{C}^{m \times n}$
• Se $M\in\mathbb{C}^{m\times p}$, $x\in\mathbb{C}^{p}$ então $Mx\in \mathbb{C}^{p}$;

Importante: no Octave/Matlab, utiliza-se $\ast$ para o produto entre matrizes e produto matriz-vetor. Percebam que esse produto só está definido se o número de colunas da matriz à esquerda no produto é o mesmo número de linhas da matriz à direita no produto. A comutatividade não é sempre válida.

• Se $M,N \in \mathbb{C}^{p\times q}$ tais que seus elementos são $M=[m_{ij}]_{i=1,j=1}^{p,q}$ e $N=[n_{ij}]_{i=1,j=1}^{p,q}$
  • $M+N = [m_{ij}+m_{ij}]_{i=1,j=1}^{p,q}$
  • $M \odot N = [m_{ij} \cdot m_{ij}]_{i=1,j=1}^{p,q}$ (produto de Hadamard - no Octave/Matlab, utiliza-se $.\ast$, isto é, $M.\ast N$)

Exercícios¶

1) Considere as matrizes $A \in \mathbb{C}^{3 \times 2}, B \in \mathbb{C}^{2 \times 3}, C \in \mathbb{C}^{3 \times 3}, x \in \mathbb{C}^{2}, y \in \mathbb{C}^{3}\text{ e }z \in \mathbb{C}^{5}.$ Faça:

$ \ \ \ \ \ \ $ a) $AB$. $ \ \ \ $ b) $CA$. $ \ \ \ $ c) $A^TC$. $ \ \ \ $ d) $BC$. $ \ \ \ $ e) $3A^T+\frac{1}{2}B$. $ \ \ \ $ f) $B\odot A^T$. $ \ \ \ $ g) $Ax$. $ \ \ \ \ $ h) $By$. $ \ \ \ \ $ i) $[x^T \ y^T]z$

String ¶

String são caracteres organizados na forma de um vetor. Para criá-la, digitamos os caracteres entre aspas simples (’) ou duplas ("):

• Strings podem conter números, letras, símbolos etc.
• Para usar aspas como uma string é necessário duas aspas dentro do corpo da string.

O fato de string ser um vetor nos permite o mesmo tratamento que temos feito até o momento. Assim podemos referenciar, adicionar e eliminar elementos da string e criar matrizes de strings.

Vejamos os exemplos a seguir:

Algumas funções nativas do Matlab/Octave ¶

• zeros(m,n): retorna uma matriz nula com $m$ linhas e $n$ colunas.
• ones(m,n): retorna uma matriz com todos os elementos igual a 1, com $m$ linhas e $n$ colunas.
• eye(m,n): retorna uma matriz com a diagonal principal com elementos iguais a 1 e os outros elementos iguais a zero, com $m$ linhas e $n$ colunas.
• length(A): retorna o número de elementos no vetor $A$.
• size(A): retorna um vetor linha $[m,n]$ onde $m$ e $n$ representam a dimensão da linha e coluna respectivamente.
• reshape(A,m,n): rearranja uma matriz $A$ com $r$ linhas e $s$ colunas para $m$ linhas e $n$ colunas. $r$ vezes $s$ deve ser numericamente igual a $m$ vezes $n$.
• diag(v): quando $v$ é um vetor, cria uma matriz quadrada contendo os elementos de $v$ na diagonal principal. Quando $v$ é uma matriz, cria um vetor coluna a partir dos elementos na diagonal principal.
• round(v): quando $v$ é uma matriz, os elementos são arredondados para o inteiro mais próximo, no caso de a parte fracion ́aria ser igual a 0,5 o elemento é arredondado para o inteiro maior.
• rand ou rand(): retorna um número aleatório entre $0$ e $1$.
• rand(m,n): retorna uma matriz $m \times n$ com elementos aleatórios entre $0$ e $1$.
• randperm(n): retorna um vetor linha com $n$ elementos que são a permutação aleatória dos inteiros de $1$ até $n$.
• randn(m,n): retorna uma matriz $m \times n$ com média $0$ e desvio-padrão 1.
• median(A): se $A$ é um vetor, retorna o valor mediano dos elementos do vetor.
• mean(A): se $A$ é um vetor, retorna o valor médio dos elementos do vetor. Se $A$ é uma matriz retorna um vetor linha com a media de cada coluna.
• sort(A): se $A$ é um vetor, ordena os elementos de $A$ na ordem crescente. Se $A$ é uma matriz, ordena os elementos de cada coluna.
• C = max(A): se $A$ é um vetor, $C$ receberá o maior elemento de $A$. Se $A$ é uma matriz, $C$ é um vetor linha contendo o maior elemento em cada coluna de $A$.
• [d n]=max(A): se $A$ é um vetor, $d$ recebe o maior elemento de $A$ e $n$ indica a posição desse elemento no vetor (a primeira posição, caso o elemento não seja único).
• min(A): semelhante à função $max(A)$, porém retorna o minimo.
• [d,n]=min(A): semelhante à função $[d,n]=max(A)$, porém retorna o minimo.
• sum(A): se $A$ é um vetor, retorna a soma dos elementos do vetor. Se $A$ é uma matriz retorna um vetor linha com a soma de cada coluna.
• std(A): se $A$ é um vetor, retorna o desvio-padrão dos elementos do vetor.
• det(A): retorna o determinante da matriz quadrada $A$.
• dot(a,b): determina o produto escalar de dois vetores $a$ e $b$.
• cross(a,b): determina o produto vetorial de dois vetores $a$ e $b$. Os dois vetores devem possuir três elementos.

Sistema linear ¶

O sistema linear é uma coleção de equações com uma ou mais variáveis. Um sistema linear, geral, com $m$ equações e $n$ incógnitas é como dado a seguir:

Pela definição de produto matriz-vetor, é fácil perceber que o sistema linear acima pode ser representado pelo produto matriz-vetor $Ax=b$, em que

Portanto, a solução do sistema linear, quando existe, pode ser obtida isolando o vetor $x$ de um lado da igualdade $Ax=b$. Se $A$ é uma matriz quadrada e inversível, a solução do sistema é dada por $$x=A^{-1}b.$$ No Octave/Matlab, para resolver um sistema linar que tenha solução, basta representa-lo no formato matricial e, utilizar o operador $\setminus$, que vimos anteriormente. Esse operador escolhe a forma mais eficiente de resolver esse sistema.

obs: podíamos, aqui, dizer que para resolver um sistema, bastava encontrar a matriz inversa de $A$, $A^{-1}$ e fazer $x=A^{-1}b$. O Matlab até tem uma função que encontra essa inversa ($inv(A)$, ou simplesmente $A^{-1}$). Mas como encontrar essa inversa é muito caro computacionalmente, e pode levar a erros numéricos de ponto flutuante, existem métodos mais eficientes de se obter a solução de sistemas lineares (como fatoração $QR$, $SVD$ ...). Vejamos...

Exemplo¶

Considere o sistema

Observe que é possível representar o sistema de equações acima como uma igualdade entre dois vetore, $$Ax=b,$$ em que $$A= \left(\begin{array}{ccc}1 & -1 & 2 \\ -1 & 1 & -1 \\ 3 & 5 & 7 \end{array}\right), x=\left(\begin{array}{c} x \\ y \\ z\end{array}\right)\text{ e }b= \left(\begin{array}{c}5 \\ -3 \\ -1\end{array}\right).$$

Colocando em variáveis no Octave/Matlab, podemos encontrar a solução $x=\left(\begin{array}{r}-\frac{5}{4} \\ -\frac{9}{4} \\ 2\end{array}\right)$ como segue:

Plotando gráficos ¶

Suponha que queiramos imprimir o gráfico da função $f(x)=\sin{(x)}$. Em nosso primeiro teste, vamos aplicar a função seno no conjunto $\left\{0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}, 2\pi\right\}$. Ao aplicar a função seno em cada um dos pontos desse domínio, obtemos o vetor $ \left\{\sin (0), \sin \left( \frac{\pi}{2}\right), \sin(\pi), \sin\left( \frac{3\pi}{2}\right), \sin(2\pi)\right\}=\{0, 1, -1, 0\}$.

Para imprimirmos esse resultado, utilizaremos a função plot em sua sintaxe mais simples:

plot(D,f(D))

em que $D$ é o domínio do gráfico e f(D) é a imagem da função, no domínio especificado. Na próxima célula definiremos os conjuntos $D$, o conjunto $FD=\sin(D)$ e plotaremos esse resultado.

Note que esse não é exatamente o gráfico do seno que conhecemos, mas sim uma aproximação. O comando plot liga cada ponto $(x, f (x))$, e como nesse caso só temos 5 pontos, o gráfico terá apenas 5 pontos.

Vamos usar o comando linspace para criar um vetor com uma quantidade grande o suficientede elementos. Por exemplo, se quisermos um vetor de 50 elementos:

Isso fará com que $x$ seja o vetor que tem $0$ como primeiro, elemento, $2\pi$ como último elemento, e $48$ elementos entre eles. Por fim, criamos o vetor com o seno aplicado a cada elemento de x e o plotamos

O Octave/Matlab te dá algumas possibilidades de plot 2D. Com a função plot, você poderá plotar mais de um gráfico em uma única janela, ou plotar em subjanelas, adicionar título, legenda, alterar o formato do domínio e imagem, etc. Aqui vamos explorar algumas possibilidades. Fique livre em explorar outras possibilidades.

Mult-line plots¶

Caso necessite plotar dois gráficos de um mesmo domínio em uma só janela, com a função plot é possível. Para isso, basta adicionar mais elementos na função, a ver

plot(D,I1,D,I2,...,D,In)

Você pode, ainda, utilizar a sintaxe

plot(D,F(D))
hold on
plot(D,G(D))
hold on
plot(D,H(D))
hold off

para plotar diversos gráficos em uma mesma janela.

Subplots¶

A sintaxe para criar subplots, ou seja, multiplos plots em diferentes janelas, é

subplot(m,n,p)

em que $m$ é o número de linhas, $n$ é o número de colunas e $p$ é a posição em que o gráfico irá ocupar. Para ilustrar melhor, vamos observar a seguinte imagem (Fonte: http://matlab.izmiran.ru/help/techdoc/ref/subplot.html):

Observe que, o plot nomeado como subplot 221 é o gráfico na posição $p=1$, de um conjunto de gráficos 4 gráficos, em uma "matriz de gráficos" $m\times n$, com $m=n=2$. Confuso? SIM :( Vamos para a prática.

Plot a partir de matrizes¶

Você pode armazenar todos os gráficos que queira imprimir em uma mesma janela em uma matriz e aplicar a função plot nela:

Design dos plots¶

É possível mudar o design dos gráficos. Você poderá alterar as cores das linhas e até o formato da linha (pontilhado, tracejado, etc). A sintaxe pode ser:

plot(D,F(D),'opcao 1','opcao 2', ... , 'opcao n',D, G(D), 'opcao n+1','opcao n+2',...)

em que $D$ é o domínio do seu gráfico, $F(D)/G(D)$ são as imagens, e $'opcao \ k'$ são as opções de design que você escolher.

Algumas das opções podem ser vistas nas tabelas a seguir:

Cores¶

Nome	código	cor
Vermelho	'r'
Verde	'g'
Azul	'b'
Ciano	'c'
Magenta	'm'
Amarelo	'y'
Preto	'k'
Branco	'w'

É possível, ainda, utilizar a sintaxe

plot(D,FD,'Color',RGB_code)

para utilizar a cor que desejar. Por exemplo:

Linestile e Marker¶

Linestile¶

Descrição	Código	Resultado
Linha sólida (padrão)	'$-$'
Tracejado	'$- -$'
Pontilhado	':'
Traço e ponto	'$- .$'

Mark¶

Vamos ver alguns exemplos:

Outros parâmetros do plot¶

A função plot tem alguns outros parâmetros que podem ser adicionados à janela do gráfico, como legenda, título, rótulo dos eixos, tamanho, etc. Vejamos alguns desses parâmetros:

plot(D,F(D),D,G(D), ... , D, Z(D));
title('...'); % Título do gráfico
legend(['...',...,'...']); % Legenda dos gráficos que compõe a janela do plot.
xlabel('...'); % Define o rótulo do eixo x
ylabel('...'); % Define o rótulo do eixo y
xlim([a b]); % Define o subdomínio do eixo x a ser exibido no gráfico
ylim([a b]); % Define o subdomínio do eixo y a ser exibido no gráfico

Cálculo no Octave ¶

Neste módulo, vamos precisar de um pacote para Octave chamado "Symbolic". Nele, poderemos fazer cálculos simbólicos, isto é, utilizar x como variável. É possível que no Matlab já venha instalado. Caso esteja usando Octave, será necessário fazer algumas instalações antes.

Instalação ¶

1. Verifique sua instalação de Python (https://www.python.org/) e SymPy (https://www.sympy.org/en/index.html). Caso não os tenha instalados no seu computador, por favor, verifique como instalar eles corretamente. O SymPy necessário para que o Symbolic do Octave rode corretamente é a versão 1.5.1. Caso você instale uma versão posterior, será necessário fazer o downgrade.

UBUNTU/macOS

Verifique q versão do seu python instalado fazendo

python --version

Caso não tenha o Python3.9 instalado no seu computador faça

sudo apt update
sudo apt install python3.9

Instale o PIP:

curl https://bootstrap.pypa.io/get-pip.py -o get-pip.py
python3.9 get-pip.py

Instale o Sympy (v. 1.5.1)

pip3.9 install sympy==1.5.1

1. Abra o Octave e execute

   pkg install -forge symbolic
   pkg load symbolic
   

WINDOWS

• Download symbolic-win-py-bundle-2.7.0.zip em https://github.com/cbm755/octsympy/releases

• Abra o octave e execute

  pkg install symbolic-win-py-bundle-2.7.0.zip
  pkg load symbolic
  

O objetivo da matemática simbólica, aqui, é para simularmos a continuidade de funções. Lembre-se que no computador, trabalhamos com matemática discreta. Assim, a definição de limite, derivada e integral, como conhecemos, não se aplica aqui. Por isso é necessário utilizar da simulação de continuidade para efetuarmos os cálculos dessas funções.

Ao instalar com sucesso o pacote de matemática simbólica em seu computador, utilizaremos uma função deste pacote chamada syms, para declarar a variável que iremos referenciar.

No seu Octave, digite:

Após definirmos nossa função simbólica, podemos definir nossas funções. Para definir a função $f(x)=\sqrt{\frac{1}{x^2+1}}$, fazemos

Limite ¶

Para calcularmos o Limite na função $f(x)$ acima, utilizaremos a função limit, cuja sintaxe é

limit(fx,x,a)

em que fx é a função que queremos calcular o limite, x é a variável a se aplicar esse limite e a é o escalar tal que $x\to a$. Por exemplo:

Derivada ¶

Para o cálculo da $n$-ésima derivada da função $f(x)$ utilizaremos a função diff cuja sintaxe é

diff(fx,n)

em que fx é a função que queremos calcular e n é o grau da derivada que queremos calcular. No octave, obtemos:

É possível avaliar o valor das derivadas (e das funções) nos pontos desejados. Para isso, utilizaremos a função subs, cuja sintaxe é

x=k;
subs(fx)

em que x é a variável que queremos avaliar, k é o valor em que substituiremos o $x$ e fx é a função. Por exemplo:

Integrais ¶

Para calcularmos integrais indefinidas, devemos usar a função int, cuja sintaxe é

int(fx)

em que fx é a função que queremos avaliar. No octave, a integral indefinida da função $$g(x)=\int \ln{x}-x^3 dx$$ fica

Para calcularmos integrais definidas, utilizaremos a mesma função anterior, adicionando os limites de integração na sintaxe. Ou seja, para calcular $$\int\limits_{a}^{b}f(x)dx,$$ utiliza-se a sintaxe

int(fx,a,b)

onde fx é a função que queremos avaliar, a é o limite inferior e b é o limite superior. No octave:

Gráficos das funções simbólicas ¶

Muitas vezes, tem-se a necessidade de visualizarmos as funções que estamos trabalhando. Assim, para plotarmos os gráficos de funções simbólicas, utilizaremos a função ezplot, cuja sintaxe é

ezplot(fx,DOM)

em que fx é a função que queremos visualizar e DOM é um vetor linha de 2 variáveis $DOM=[xmin xmax]$, que definirá o domínio da função. No octave:

Programação ¶

Um algoritmo é uma sequência finita de ações executáveis, precisos e não ambíguos a fim de obter uma solução para um determinado problema. Já a linguagem de programação traduz um algoritmo (sequência de instruções/ações) da linguagem humana para a linguagem de máquina.

Uma maneira eficiente de projetar um algorítmo é por meio de um pseudo código. Por exemplo, se eu quero escrever um algoritmo que devolve o módulo de um número, em qualquer linguagem de programação, seu pseudo código pode ser escrito da seguinte forma:

Dado um número a
Se a >= 0, então
    modulo = a
Senão
    modulo=-a
retorna modulo

Em C++, por exemplo, o algorítmo acima poderia ser escrita como uma função, e ficaria assim:

double modulo(double x){
    double m;
    if (x >= 0){
        m = x;
    } else {
        m = -x;
    }
    return m;
}

Em Python, por exemplo, esse mesma função ficaria

def modulo(x):
    if x>=0:
        m = x
    else:
        m = -x
    return m

Cada linguagem de programação tem suas características. No Matlab/Octave, por exemplo, a mesma função acima ficaria:

Algumas observações importantes na hora de criarmos nossos algoritmos aqui no Octave/Matlab:

• Todo texto depois de % é considerado um comentário;
• O caractere ... indica que o comando continua na próxima linha. Tal recurso permite deixar o texto mais organizado;
• Usa-se o ponto e vírgula ; (lembra dele?) no final de uma linha de comando. Ele omite na janela de comandos as iterações que serão realizadas (mantém a janela de comando mais limpa e organizada);
• Pode-se colocar mais de um comando em uma linha, separando-os por ponto e vírgula;
• Os nomes das variáveis devem ser palavras únicas, sem inclusão de espaços e devem começar com uma letra, seguida de letras ou números, podendo conter até $19$ caracteres;
• Para a entrada de dados via teclado usa-se a função input;
• Para mostrar mensagens de texto na tela utiliza-se o comando disp.
• Você pode usar a função tic/toc para contar o tempo de execução do algoritmo. Por exemplo:

  tic;
  % algoritmo
  toc;
  

Comando lógico-relacionais ¶

OBS: Operações curto-circuito

• expr1 && expr2 representa a operação lógica ... e ... e aplica um comportamento de curto circuito no código. Isto é, $expr2$ não é avaliada se $expr1$ é falso.

• expr1 || expr2 representa a operação lógica ... ou ... e aplica um comportamento de curto circuito no código. Isto é, $expr2$ não é avaliada se $expr1$ for verdadeira.

O Octave/Matlab possui estruturas que permitem o controle do fluxo de execução de comandos e da ordem em que a computação é feita.

Laço FOR ¶

A estrutura FOR possibilita que um bloco de código seja repetido por um número de vezes fixo e predefinido. Sua sintaxe é:

for variável = início:passo:fim
    % comandos
end

Exemplo¶

1) Faça um algoritmo usando laço FOR que retorne a soma dos números de $1$ a $N$, em que $N$ é dado pelo usuário.

OBS: Laços for nem sempre são a melhor forma de construir um algoritmo, em Matlab/Octave. Vou escrever o mesmo algorimo acima usando vetores e funções nativas. Vamos comparar os tempos.

Laço WHILE ¶

A estrutura while é utilizada quando é necessário repetir certo comando de código várias vezes, enquanto uma determinada condição é satisfeita. Geralmente, usa-se while quando não se sabe ao certo a quantidade de passos a serem dados pelo algoritmo. Sintaxe:

while expressão
    comandos
end

Exemplo¶

1) Encontre o menor número $n\in\mathbb{N}\cup\{0\}$ tal que $\frac{1}{2^n} < 10^{-12}$ .

2) Encontre o menor número natural tal que $\sqrt[n]{n} < 1 + 10^{-5}$.

3) Encontre o menor número, maior ou igual a um $N$ fornecido pelo usuário que é múltiplo de $7$.

If, Elseif e Else ¶

A estrutura if é usada para executar um bloco de comandos apenas se uma determinada condição for satisfeita. Sintaxe:

if expressão1
    % comandos 1
elseif expressão2
    % comandos 2
elseif expressão3
    % comandos 3
else
    % comandos 4
end

Exemplo¶

1) Faça um programa que diga se a pessoa é adulta, adolescente, criança ou idosa, com base na idade fornecida. Use o comando While para fazer o usuário digitar uma idade maior do que zero.

Switch, case, otherwise ¶

O switch executa uma ação dentre várias opções, dependendo de um parâmetro passado inicialmente, onde cada escolha é um caso. Sintaxe:

switch variável_de_teste
case{caso1}
    % comandos1
case{caso2}
    % comandos2
case{caso3}
    % comandos3
otherwise
    % comandos
end

Exemplo¶

1) Construa um programa onde o usuário digita dois números e indica se irá somá-los, multiplicá-los ou subtraí-los.

Funções ¶

Muitas vezes não será necessário criarmos uma nova função, pois o Octave/MATLAB já nos traz uma grande biblioteca de funções pré-definidas. Por exemplo: se quisermos calcular o fatorial de um número $n$, não é necessário criar uma nova função para isso, basta usarmos a função

factorial(n).

Algumas funções pré-definidas no Octave/MATLAB:

Muitas vezes queremos criar funções que ainda não estão na biblioteca virtual do Octave/MATLAB. Para isso temos o comando $function$, que obedece a seguinte sintaxe:

function[saida] = nomedafuncao(entrada)
    % Comentário da função, que aparecerá quando fizer '>>> help nomedafuncao'
    <comandos>
end

Exemplo¶

Dados dois números, queremos uma função que nos retorne a soma e o produto dos dois. Vamos utilizar o function:

Agora basta salvar o arquivo como somaprod.m. Para executar a função, basta digitarmos no Octave/MatLab que o propgrama irá retornar os vaores de soma e produto. Vale lembrar que, quando uma função retorna 2 ou mais valores, é possível solicitar apenas um deles, como veremos na célula abaixo.